치환 $\sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&8&6&7&4&1&5&2 \end{pmatrix}$가 있다고 하자.
이 치환을 반복하다보면 유한번(최대 치환 크기)안에 처음 원소 순서로 돌아온다.
$\sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&8&6&7&4&1&5&2 \end{pmatrix}$
$\sigma^2 = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 6&2&1&5&7&3&4&8 \end{pmatrix}$
$\sigma^3 = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 1&8&3&4&5&6&7&2 \end{pmatrix}$
$\sigma^4 = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&2&6&7&4&1&5&8 \end{pmatrix}$
$\sigma^5 = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 6&8&1&5&7&3&4&2 \end{pmatrix}$
$\sigma^6 = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 1&2&3&4&5&6&7&8 \end{pmatrix}$
이 경우는 6번만에 원래대로 돌아왔다.
관찰해보면 각 숫자들은 다음과 같이 순환하는 형태를 띈다.
$1\rightarrow3\rightarrow6\rightarrow1\rightarrow\cdots$
$2\rightarrow8\rightarrow2\rightarrow\cdots$
$3\rightarrow6\rightarrow1\rightarrow3\rightarrow\cdots$
$4\rightarrow7\rightarrow5\rightarrow4\rightarrow\cdots$
$5\rightarrow4\rightarrow7\rightarrow5\rightarrow\cdots$
$6\rightarrow1\rightarrow3\rightarrow6\rightarrow\cdots$
$7\rightarrow5\rightarrow4\rightarrow4\rightarrow\cdots$
$8\rightarrow2\rightarrow8\rightarrow\cdots$
각각을 궤도(orbits)라고 한다.
위 치환에서 궤도는 다음과 같이 3개로 이루어져있다.
$\{1,3,6\}, \{2,8\}, \{4,7,5\}$
각각 3개, 2개, 3개의 원소를 가진 궤도라고 한다.
이를 그래프로 나타내면 서로 공통된 부분이 없는 단순 사이클인 방향그래프가 될 것이다.
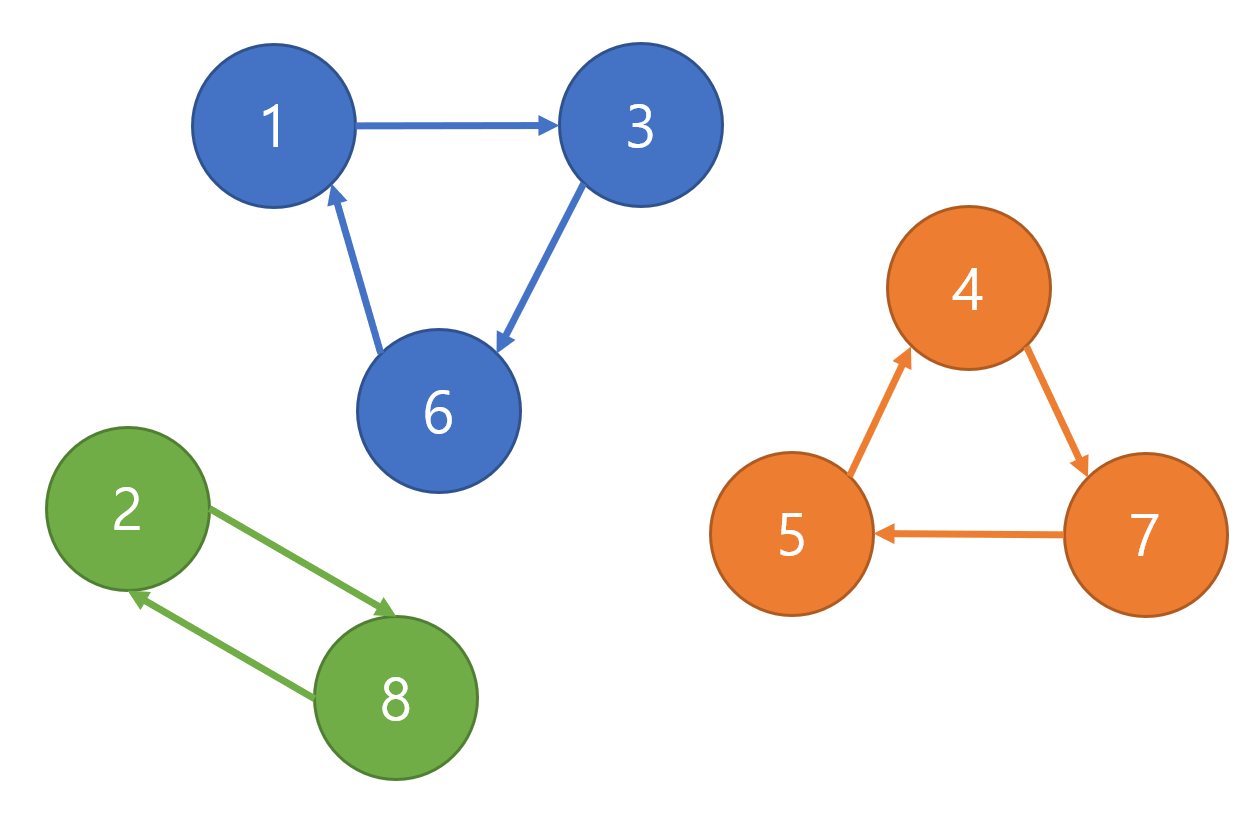
다음 치환을 살펴보자
$\sigma = \begin{pmatrix} 1&2&3&4&5 \\ 2&1&3&4&5 \end{pmatrix}$
이는 궤도가 $\{1,2\}, \{3\}, \{4\}, \{5\}$로 이루어진다.
이 치환은 길이가 $\{1,2\}$말고는 모두 원소가 1인 궤도이다.
이렇듯 원소가 2 이상인 궤도가 많아야 하나뿐일 때 $\sigma$를 순환치환(cycle) 이라고 하고 가장 큰 궤도에 있는 원소의 개수가 순환치환의 개수(length)이다.
그리고 위의 치환에서 $\sigma = (1,2) = (2,1)$로 간단하게 나타낼 수 있다.
가장 처음 나타낸 치환은 아래와 같이 순환치환의 곱으로 나타낼 수 있다.
$\sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&8&6&7&4&1&5&2 \end{pmatrix} = (1,3,6)(2,8)(4,5,7)$
그리고 이러한 순환치환들은 서로에게 영향을 미치지 않기 때문에 서로 소(disjoint)라고 부른다.
이런점에서 모든 유한집합의 치환들은 여러개의 서로 소인 순환치환들의 곱으로 나타낼 수 있다.
또한 순환치환은 위 그림에서 하나의 사이클을 나타내기 때문에 여러개의 서로소인 순환치환은 가환이된다.
특히 개수가 2개인 순환치환을 호환(transposition)이라고 한다.
순환치환은 아래와 같이 호환의 곱으로 나타낼 수 있다.
$(a_1, a_2, \cdots , a_n) = (a_1, a_n)(a_1,a_{n-1})\cdots(a_1, a_3)(a_1, a_2)$
모든 유한 치환은 서로 소인 순환치환들의 곱으로 나타낼 수 있고 순환치환은 호환의 곱으로 나타낼 수 있으니 모든 유한 치환은 호환의 곱으로 나타낼 수 있게 된다.
$\sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&8&6&7&4&1&5&2 \end{pmatrix}$
$= (1,3,6)(2,8)(4,7,5) = (1,6)(1,3)(2,8)(4,5)(4,7)$
위의 치환에서 호환의 개수는 5개(홀수)이다.
각 치환은 호환의 곱으로 나타낼 수 있는 방법이 여러가지가 있는데 호환의 개수가 짝수개로만 또는 홀수개로만 나타낼 수 있다.
위 예시는 홀수개였으므로 다르게 나타냈을 때 짝수개가 나올 수 없다는 뜻이다.
이런 점에서 호환의 개수가 짝수개인 치환을 우치환(even), 홀수개인 치환을 기치환(odd)이라고 한다.
$\sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8 \\ 3&8&6&7&4&1&5&2 \end{pmatrix}$는 기치환의 예이다.
그리고 가장 간단한 항등치환은 $(1,2)(1,2)$이다.
크기가 2 이상인 치환에 대해서 정의되며 언제나 우치환이 된다.
그리고 $n$개의 문자에 대한 우치환으로 구성된 $S_n$의 부분군 $A_n$을 $n$문자에 대한 교대군(Alternating Group) 이라고 한다.
'수학 > 현대대수학' 카테고리의 다른 글
| [현대대수학] Resultant 활용 - 음함수 찾기 (0) | 2023.10.15 |
|---|---|
| [현대대수학] Sylvester 행렬과 Resultant (0) | 2023.10.14 |
| [현대대수학] 8. 치환군 (0) | 2021.12.23 |
| [현대대수학] 7. 생성집합 (0) | 2021.12.20 |
| [현대대수학] 6. 순환군 (0) | 2021.12.14 |