학교에서 수학과의 정수론(학교에서의 과목이름은 수론)과목이 전공 인정이 되어 이번에 수강하게 되었다.
시험정리도 하고 알고리즘 정수론 태그 공부도 할 겸해서 포스팅을 하려고 한다.
피타고라스 정리
$a^2 + b^2 = c^2 (a,b,c \in \mathbb{R})$
위 식은 잘 알려져 있다.
여기서 $(a,b,c) \in \mathbb{N}$으로 범위를 좁혀서 생각해보자.
피타고라스 정리에서 양변을 $c^2$로 나누면 식이 다음과 같이 된다.
$\frac{a^2}{c^2} + \frac{b^2}{c^2} = 1$
이는 단위원 $x^2 + y^2 = 1$에서 $x = \frac{a}{c}, y= \frac{b}{c}$인 점을 나타낸다.
여기서 $x,y$는 유리수가 나오므로 피타고라스 세 쌍은 단위원에서 유리수 점을 나타내게 된다.
단위원에 존재하는 유리수점은 무한하므로 자연수 범위에 존재하는 피타고라스 세 쌍은 무한히 존재한다.
단순히 생각해도 무한하다는 것을 증명 할 수 있다.
우선 자명한 피타고라스 쌍 $(3, 4, 5)$를 생각해보자.
$k \in \mathbb{N}$가 존재하여 $(3k,4k,5k)$도 피타고라스 쌍이다.
$k$가 무한하므로 피타고라스 쌍도 무한하다는 것을 보일 수 있다.
그럼 여기서 의미있는 결과를 도출하려면 $\gcd(a,b,c) = 1$ 즉 모두가 서로소인 피타고라스 세 쌍을 관찰해야 한다.
>> Theorem) $\{(x,y)\in \mathbb{Q}^2 : x^2+y^2=1 \} = \{(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}):t \in \mathbb{Q}\} \cup \{(-1,0)\} $
proof
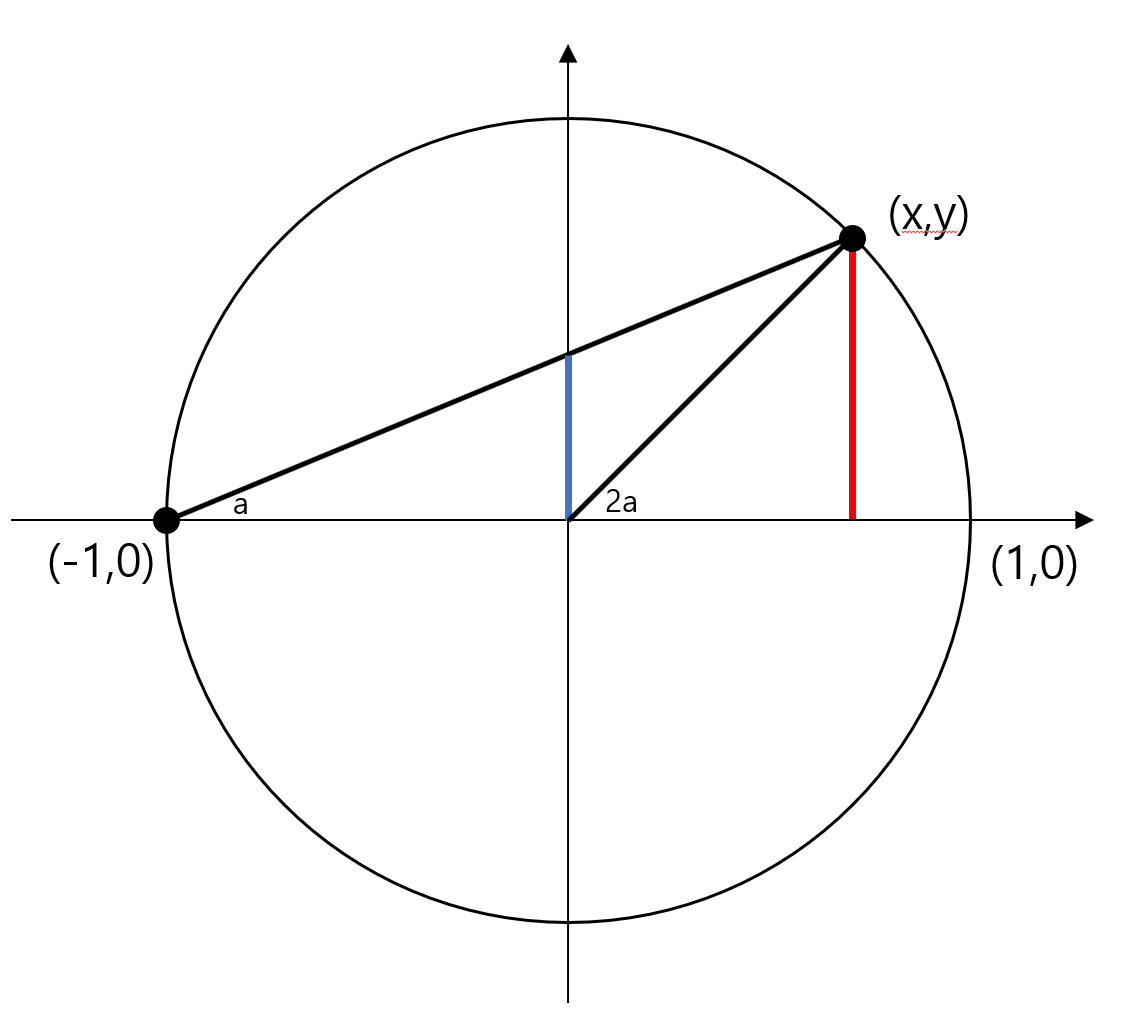
위 원에서 $(x,y)$는 유리수이고 파란 선의 길이를 $t$라고 하면 $t = \tan a$이고 유리수이다. (직선의 방정식)
$x = \cos 2a, y= \sin 2a$이고 $t = \frac{y}{1+x}$라고 볼 수 있다.
우선 $\cos^2 a = \frac{1}{1+\tan^2 a} = \frac{1}{1+t^2}$를 기억하자.
$x = \cos 2a = 2\cos^2 a - 1 = 2\frac{1}{1+t^2}-1 = \frac{1-t^2}{1+t^2}$
$y = t(1+x) = t\frac{1-t^2+1+t^2}{1+t^2} =\frac{2t}{1+t^2}$
여기서 $(x,y) = (-1,0)$을 만들 수 없으므로 따로 추가해준다.
따라서 단위원위의 유리수 점 $(x,y)$에 대응하는 유리수 $t$가 존재하여 유리매개화를 할 수 있다. $\Box$
> Lemma) $\gcd(n,m) = 1$ 이면 $\gcd(n^2+m^2,n^2-m^2) \in \{1,2\}$이고 $\gcd(2nm, n^2-m^2) \in \{1,2\}$이다.
proof
$p \mid n^2-m^2, p \mid n^2+m^2$인 소수 $p$가 존재한다고 하자.
약수와 배수의 관계에 의해 $p \mid 2n^2, p \mid 2m^2$이 성립한다.
$p=2$는 자명하므로 $p \neq 2$를 생각해보면 $p \mid n^2, p\mid m^2$이고 $p \mid n, p \mid m$이다.
근데 처음에 $n,m$은 서로소라고 했다.
따라서 $p$는 $n, m$을 동시에 나눌 수 없다.
소수가 안되니 소수로 만들어진 합성수도 불가능하다.
다만 $1$일때는 언제나 나누어 떨어진다.
따라서 $\gcd(n^2+m^2,n^2-m^2) \in \{1,2\}$이다. (후자도 같은 방식으로 증명) $\Box$
>> Theorem) 모든 피타고라스 쌍은 $(p^2-q^2, 2pq, p^2+q^2) p,q \in \mathbb{N}$으로 나타낼 수 있다.
proof
위의 Theorem에서 $(x,y) = (\frac{a}{b}, \frac{b}{c}) = (\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2})$
$t$는 유리수이므로 $t=\frac{q}{p}$이라고 하면 $(\frac{a}{b}, \frac{b}{c}) = (\frac{p^2-q^2}{p^2+q^2}, \frac{2pq}{p^2+q^2})$
Lemma에 의해 $\gcd(p^2+q^2, p^2-q^2) \in \{1,2\}$이다.
만약 $1$이라고 하면 그 자체로 기약분수이기 때문에 $a = p^2-q^2, b=2pq, c=p^2+q^2$로 쓰면 된다.
$2$라고 하면 $p, q$는 홀짝성을 같게 한다.(p가 홀수이면 q도 홀수이다.)
$n = \frac{p+q}{2}, m = \frac{p-q}{2}$라고 하면 둘 다 홀수가 된다.
$p = n+m, q = n-m, p^2-q^2 = 4nm, p^2+q^2 = 2(n^2+m^2)$
즉 $\frac{a}{c} = \frac{2nm}{n^2+m^2}, \frac{b}{c} = \frac{n^2-m^2}{n^2+m^2}$
$a = 2nm, b=n^2-m^2, c=n^2+m^2$ $\Box$
실제로 $p=2, q=1$을 대입하면 $(3,4,5)$가 나오고 $p=3, q=2$를 대입하면 $(5,12,13)$이 나온다.
'수학 > 정수론' 카테고리의 다른 글
| [정수론] 6. 중국인의 나머지 정리 (0) | 2022.04.21 |
|---|---|
| [정수론] 5. 고차 합동 방정식 (0) | 2022.04.20 |
| [정수론] 4. 합동 (0) | 2022.04.17 |
| [정수론] 3. 디오판투스 방정식 (0) | 2022.04.12 |
| [정수론] 2. 유클리드 호제법 (0) | 2022.04.06 |