점근적 표기법
점근적 표기법(Asymtotic notation)은 함수의 증감 추세를 비교하는 표기법이다. 다른 말로 란다우 표기법(Landau notation)이라고도 한다. 어떤 함수의 정확한 함수식을 표현하는 것이 아닌 근접한 함수식으로 표현하는 표기법이다. 점근적 표기법으로는 대표적으로 다음과 같은 표기가 있다.
- Big-$O$: $O(g(n))$
- Big-$\Omega$: $\Omega(g(n))$
- Big-$\Theta$: $\Theta(g(n))$
- little-$o$: $o(g(n))$
- little-$\omega$: $\omega(g(n))$
We often want to know a quantity approximately, instead of exactly, in order to compare it to another.
- Donald Knuth (TAOCP vol. 1)
Big-$O$ 표기법
어떤 함수 $f(n)$이 다음 조건을 만족하는 집합에 있으면 $f(n) = O(g(n))$이라고 한다. 여기서 $=$는 "같다"의 의미가 아니라 $\in$정도로 이해하는 것이 좋다.
$O(g(n)) = \{f(n) : n_0 \le n $인 모든 $n$에 대하여 $0 \le f(n) \le c \cdot g(n)$인 양의 상수 $c, n_0$이 존재하는 $f(n) \}$
예를 들어 $f(n) = n$라고 하자. 이 $f(n)$이 들어갈 수 있는 $g(n)$의 종류에는 $n, n^2, 2^n$등등이 있다. 이 말인 즉슨 $f(n) = O(n),\ f(n) = O(n^2),\ f(n)=O(2^n)$이라고 나타낼 수 있다. 하지만 $O(\sqrt{n})$, $O(\log{n})$이라고는 나타낼 수 없다. 이를 일반화하면 가능한 $g(n)$은 다음 조건을 만족한다고도 볼 수 있다.
$\lim\limits_{n \to \infty} \frac{f(n)}{g(n)} < \infty$
Big-$O$ 표기법이 나타내는 의미는 어떤 함수 $f(n)$이 정확히 어떻게 돼 있는지는 모르겠지만 충분히 큰 $n$에서 $g(n)$을 넘지 않는다는 상한을 의미한다.
Big-$\Omega$ 표기법
어떤 함수 $f(n)$이 다음 조건을 만족하는 집합에 있으면 $f(n) = \Omega(g(n))$이라고 한다.
$\Omega(g(n)) = \{f(n) : n_0 \le n $인 모든 $n$에 대하여 $0 \le c \cdot g(n) \le f(n)$인 양의 상수 $c, n_0$이 존재하는 $f(n) \}$
Big-$\Omega$는 Big-$O$에서 $f, g$의 위치가 바꼈다. 따라서 Big-$O$와는 반대로 $f(n) = n$일 때, $f(n) = \Omega(\sqrt{n}),\ f(n) = \Omega(\log{n})$이라고 나타낼 수 있고, $\Omega(n^2),\ \Omega(2^n)$이라고 나타낼 수 없다. 이를 마찬가지로 일반화하면 가능한 $g(n)$은 다음 조건을 만족한다고도 볼 수 있다.
$\lim\limits_{n \to \infty} \frac{g(n)}{f(n)} > 0$
Big-$\Omega$ 표기법이 나타내는 의미는 어떤 함수 $f(n)$이 충분히 큰 $n$에서 $g(n)$보다 크다는 하한을 나타낸다. Big-$O$와 Big-$\Omega$는 서로 다른 영역의 함수를 나타내므로 $O(g(n)) \cup \Omega(g(n))$은 함수 전체 집합을 의미한다.
그렇다고 $O(g(n)) \cap \Omega(g(n)) \neq \varnothing$인데 위의 예시에서 $n = O(n), n = \Omega(n)$을 동시에 만족한다. 이를 나타내는 표기법은 따로 있다.
Big-$\Theta$ 표기법
어떤 함수 $f(n)$이 다음 조건을 만족하는 집합에 있으면 $f(n) = \Theta(g(n))$이라고 한다.
$\Theta(g(n)) = \{f(n) : n_0 \le n $인 모든 $n$에 대하여 $0 \le c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)$인 양의 상수 $c_1, c_2, n_0$이 존재하는 $f(n) \}$
지금까지 나온 세 가지 표기법 중 가장 엄격한 조건을 제시한다. $\Theta(g(n)) = O(g(n)) \cap \Omega(g(n))$이 성립하고 상한과 하한을 동시에 표현한다. 일반화하면 가능한 $g(n)$은 다음 조건을 만족한다고도 볼 수 있다.
$ 0 < \lim\limits_{n \to \infty} \frac{g(n)}{f(n)} < \infty$
$f(n)$이 다항함수라면 $g(n)$의 차수는 같을 수밖에 없다.
little-$o, \omega $표기법
정의는 비슷하고 등호만 뺀 것이니 간략하게 정의만 적고 넘어간다.
$o(g(n)) = \{f(n) : n_0 \le n $인 모든 $n$에 대하여 $0 \le f(n) \lt c \cdot g(n)$인 양의 상수 $c, n_0$이 존재하는 $f(n) \}$
$\omega(g(n)) = \{f(n) : n_0 \le n $인 모든 $n$에 대하여 $0 \le c \cdot g(n) \lt f(n)$인 양의 상수 $c, n_0$이 존재하는 $f(n) \}$
점근적 표기법의 성질
다음이 성립한다.
- $f(n) = O(f(n))$
- $c \cdot O(f(n)) = O(f(n))$
- $O(f(n)) + O(f(n)) = O(f(n))$
- $O(O(f(n))) = O(f(n))$
- $O(f(n))O(g(n)) = O(f(n)g(n))$
- $O(f(n)g(n)) = f(n)O(g(n))$
또한 테일러 급수(매크로린 급수)에서도 점근적 표기법을 사용할 수 있다.
$e^x = \displaystyle\sum_{n=0}^\infty \frac{1}{n!} x^n = 1 + x + \frac{1}{2!}x^2 + \cdots + \frac{1}{m!}x^m + O(x^{m + 1})$
오해와 진실
점근적 표기법은 알고리즘의 시간복잡도를 분석하기 위해 만들어진 표기법이다.
알고리즘을 가장 처음 배울 때 시간복잡도를 접하며 점근적 표기법을 배우게 된다. 사실 지금까지 점근적 표기법을 설명하면서 알고리즘에 대한 내용은 하나도 없었다. 점근적 표기법은 알고리즘의 시간복잡도만을 위한 것은 아니고 범용적으로 쓰이는 개념이다.
Big-O는 최악, Big-$\Omega$는 최선 Big-$\Theta$는 평균 시간복잡도를 의미한다.
각각 상한, 하한, 상한과 하한을 나타내기 때문에 오해하기 쉽다. 하지만 최선, 평균, 최악에 대해 각각의 점근적 표기법을 사용할 수 있으며 그 결과는 다를 수 있다.
가장 쉬운 예시로 삽입정렬을 생각해보자.
def insertion_sort(arr):
cnt = 0
n = len(arr)
for i in range(1, n):
cnt += 1
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
cnt += 1
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return cnt이 함수를 호출하면 삽입정렬을 수행하는 데 걸린 연산 수가 나온다.
삽입정렬은 이미 정렬이 되어있는 경우 가장 최선의 입력이라는 것이 알려져 있다. 실제로 최선의 입력인 정렬된 데이터를 넣고 수행 시간을 분석하면 다음과 같다.

빨간색 그래프가 실제 결과 $f(n)$인데 각 점근적 표기법의 정의에 따르면 다음과 같다.
- $c = 2, n_0 = 10$으로 정하면 Big-$O$의 정의를 만족하므로 $f(n) = O(n)$으로 볼 수 있다.
- $c = 0.5, n_0 = 10$으로 정하면 Big-$\Omega$의 정의를 만족하므로 $f(n) = \Omega(n)$으로 볼 수 있다.
- $c_1 = 0.5, c_2 = 2, n_0 = 10$으로 정하면 Big-$\Theta$의 정의를 만족하므로 $f(n) = \Theta(n)$으로 볼 수 있다.
삽입정렬에서 최악의 입력은 역방향으로 정렬된 데이터이다. 최악인 입력을 넣고 수행 시간을 분석하면 다음과 같다.

- $c = 1, n_0 = 10$으로 정하면 Big-$O$의 정의를 만족하므로 $f(n) = O(n^2)$으로 볼 수 있다.
- $c = 0.2, n_0 = 10$으로 정하면 Big-$\Omega$의 정의를 만족하므로 $f(n) = \Omega(n^2)$으로 볼 수 있다.
- $c_1 = 0.2, c_1 = 2, n_0 = 10$으로 정하면 Big-$\Theta$의 정의를 만족하므로 $f(n) = \Theta(n^2)$으로 볼 수 있다.
평균적인 입력을 위해 랜덤 데이터를 넣고 수행 시간을 분석하면 다음과 같다.
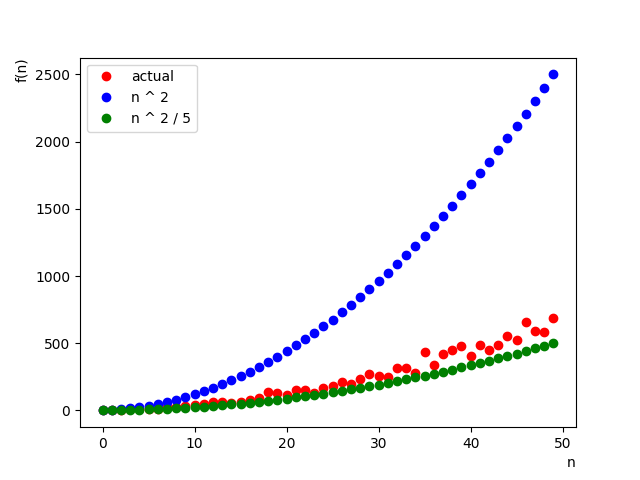
이제 좀 깔끔하지 않은 그래프가 나왔다.
- $c = 1, n_0 = 10$으로 정하면 Big-$O$의 정의를 만족하므로 $f(n) = O(n^2)$으로 볼 수 있다.
- $c = 0.2, n_0 = 10$으로 정하면 Big-$\Omega$의 정의를 만족하므로 $f(n) = \Omega(n^2)$으로 볼 수 있다.
- $c_1 = 0.2, c_1 = 2, n_0 = 10$으로 정하면 Big-$\Theta$의 정의를 만족하므로 $f(n) = \Theta(n^2)$으로 볼 수 있다.
이렇게 최선, 최악, 평균에 대해 Big-$O, \Omega, \Theta$를 정의할 수 있다. 뇌피셜이긴 하지만 주어진 알고리즘에 조건문이 없고 반복문이 입력의 크기에만 의존한다면 모든 상황에서 시간복잡도가 같아질 것 같다.
왜 Big-$O$를 많이 쓸까?
대부분의 알고리즘을 설명할 때 $O(n), O(n \log{n})$같이 Big-$O$표기법을 많이 사용한다. 여기에 대해 여러 사람들의 의견을 구했는데 다음과 같은 결론이 나왔다.
- 셋 중 유일하게 아스키코드에 들어있어서 타이핑하기 쉬웠다.
- 최악의 입력에 대한 수행시간의 상한이 다른 모든 입력을 커버할 수 있기 때문에 상한을 나타내는 Big-$O$를 사용한다.
사실 Big-$O$로 표현할 때는 위와 같이 최선, 최악, 평균에 대해 모두 정의할 수 있기 때문에 엄밀하게는 매번 "merge-sort는 최악 $O(n\log{n})$이다.", "floyd-warshall은 최악 $O(n^3)$이다." 라고 말해야 하지만 워낙 관습적으로 사용하기도 하고 많이 표현하기 때문에 "최악"을 제외하고 "merge-sort는 $O(n\log{n})$이다."라고 편하게 표현하는 것 같다.
그럼 little-$o, \omega$는 언제 쓸까?
편의상 little-$o$만 보자. 좀 심연으로 들어가면 이런 거나 이런 것 같이 이상한 시간복잡도가 나온다. 널리 알려져있는 $n \times n$ 행렬 두 개의 곱은 $O(n^3)$이지만 이 보다 빠른 알고리즘인 링크에 있는 슈트라센 알고리즘도 $O(n^{2.81})$이라고는 하지만 복잡하니 $o(n^3)$으로 볼 수 있다. 물론 $O(n^3)$도 맞는 말. 주로 $O(n^{3 - \epsilon})$같은 알고리즘을 찾을 때 $o(n^3)$이라고 쓰는 것 같다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Splay Tree를 사용해서 해결할 수 있는 유형 (2) | 2024.10.24 |
|---|---|
| [알고리즘] PS를 위한 Splay Tree (1) | 2024.10.03 |
| [알고리즘] Pollard rho 알고리즘 (0) | 2024.09.28 |
| [알고리즘] Suffix Automaton (0) | 2024.09.09 |
| [알고리즘] Push Relabel 알고리즘 (2) | 2024.08.30 |