Git은 개발할 때 없어서는 안되는 존재이다. 코드 관리, 버전 관리, 자동 병합, 브랜치 관리 등 정말 많은 기능을 수행하고 있다. 그 중 코드 관리를 살펴보고자 한다.

깃은 코드의 변화를 자동으로 추적하며 위 사진과 같이 변경된 사항을 자동으로 추적한다. 어떻게 변화한 부분만 정확히 골라서 표시하는 것일까?
LCS
LCS(Longest Common Subsequence/Substring)은 두 문자열/수열이 존재할 때 공통으로 존재하는 가장 긴 문자열/수열을 추출하는 알고리즘이다. LCS에서 S를 Substring으로 쓰면 공통된 문자열, Subsequence로 쓰면 공통된 수열이다. 둘의 차이는 공통된 요소가 연속인지 여부이다. 연속이라면 Substring, 불연속이라면 Subsequence이다. Input과는 상관 없다.
보통 잘 알려진 DP로 해결하는 LCS 문제는 Subsequence이다. Substring은 따로 Suffix 자료구조를 사용하여 구하는 정말 어려운 문제이다.
여기서는 Subsequence만 다룬다.
예를 들어 A = abcbc, B = aefcbce라면 LCS는 acbc가 된다.
Git과 LCS
그럼 Git이 코드를 추적할 때 각 문자열에서 LCS인 부분은 변화가 없다고 판단하고 그렇지 않은 부분은 변화라고 판단하면 될까?
위 아이디어는 어느정도 맞는 것 같다.
또 다시 위의 예시로 돌아가면 A가 변경 전의 코드, B가 변경 후의 코드라고 본다면 아래와 같게 추적이 될 것이다.
A = abcbc
B = aefcbce
빨간 부분이 사라진 코드, 초록 부분이 생겨난 코드이다.
즉, 변경 전 코드에서 LCS가 아닌 부분은 사라진 코드이고 변경 후 코드에서 LCS가 아닌 부분은 새로 생긴 코드이다.
실제로 https://www.acmicpc.net/problem/9252 를 해결한 코드로 시각화를 해 보았다.
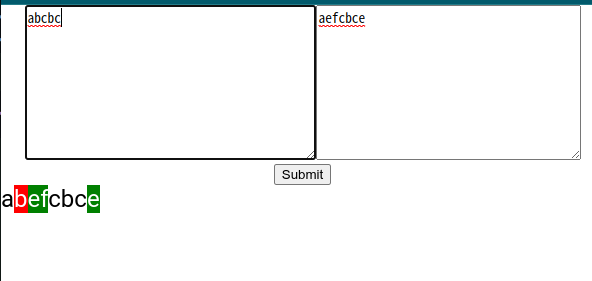
잘 된 것 같다. 그렇다면 긴 코드에 대해서도 잘 작동할까?

변경 전: 세그먼트 트리, 변경 후: 레이지 세그먼트 트리 코드이다. 뭔가 난잡하게 되어있다.
아마 문제점은 LCS를 철자 단위로 실행해서 그런 것 같다. Git은 위의 사진에서 볼 수 있는 것처럼 철자 단위로 변경을 추적하는 것이 아니라 라인/단어 단위로 추적을 한다.
그래서 라인 단위 LCS로 변경해서 다시 실행시키면

정말 Git과 유사하게 동작하는 것을 볼 수 있다.
하지만 위에서 사용한 잘 알려진 LCS알고리즘은 $O(N^2)$으로 코드 바이트 수가 10만이 넘어가면 사용하기 힘들다. 실제로 Git을 사용하며 개발할 때는 10만바이트가 넘는 코드를 작성할 수 있다. 그래서 더 효율적인 LCS알고리즘이 필요하고 그 알고리즘은 히르쉬버그?라는 기법을 사용한다고 한다. 물론 나는 모른다. 아래 문제를 해결할 수 있는 알고리즘을 사용하면 훨씬 긴 코드도 처리할 수 있다.
https://www.acmicpc.net/problem/18440
18440번: LCS 7
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
Git은 해당 기법을 사용하여 구현되었을 것이다.
시각화하는데 사용된 LCS 코드
def lcs(a, b):
arr = [[0] * (len(a) + 1) for _ in range((len(b) + 1))]
la = len(a)
lb = len(b)
for i in range(1, lb + 1):
for j in range(1, la + 1):
if a[j - 1] == b[i - 1]:
arr[i][j] = arr[i - 1][j - 1] + 1
else:
arr[i][j] = max(arr[i - 1][j], arr[i][j - 1])
a, b = b, a
i = len(a)
j = len(b)
aa = list()
bb = list()
while i and j:
if a[i - 1] == b[j - 1]:
aa.append(i-1)
bb.append(j-1)
i -= 1
j -= 1
else:
if arr[i - 1][j] > arr[i][j - 1]:
i -= 1
else:
j -= 1
return bb, aahttps://lcs.riroan.com 에서 테스트할 수 있다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] ICPC 2023 + 코드포스 퍼플 후기 (1) | 2023.12.05 |
|---|---|
| [알고리즘] KUPC 2023 출제 후기 (1) | 2023.12.02 |
| [알고리즘] 현대모비스 알고리즘 경진대회 2023 본선 (2) | 2023.07.08 |
| [알고리즘] 백준 대회 1등해서 자랑하려고 쓴 글 (8) | 2023.07.06 |
| [알고리즘] 현대모비스 알고리즘 경진대회 2023 예선 (0) | 2023.07.03 |