Pigeonhole Principle (비둘기집 원리)
Pumping Lemma를 위해 Pigeonhole Principle을 먼저 소개한다.
$N+1$개의 변수를 $N$개의 공간에 넣으면 적어도 하나의 공간에 $2$개의 변수가 있다.
너무 당연한 말이라 직관적으로 생각하기 쉽고 간단한 원리이다.
위에서는 $N+1$개의 변수라고 했는데 이를 일반화 할 수 있다.
Pumping Lemma (for DFA)
여러 종류의 머신에 대한 Pumping Lemma가 있는데 지금 우리는 DFA만 알고 있으니까 DFA용 Pumping Lemma를 알아보자. (튜링머신은 너무 복잡해서 Pumping Lemma를 적용하기 힘들다.)
$N$개의 상태를 가지는 어떤 DFA M이 길이가 $N$인 String을 AC하면 무한히 많은 String을 AC할 수 있다.
Pumping Lemma는 살짝 어려워 보이니 지난시간에 사용한 DFA를 예로 들어보자.
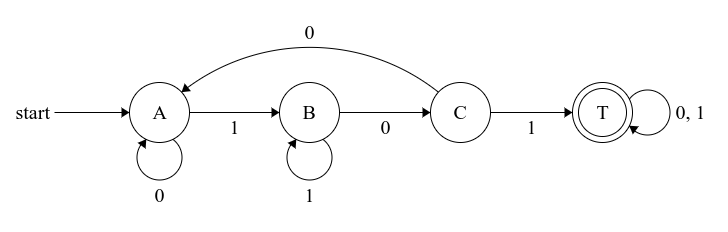
Problem X3을 AC하는 DFA이다. ($T$는 Terminal의 T)
위 DFA는 상태를 4개 가진다.
그리고 $1010 \in L3$이므로 길이가 4인 String를 AC한다.
따라서 Pumping Lemma에 의해 길이가 무한한 String도 AC한다.
관찰해보면 $1010$을 DFA에 넣으면 $ A \rightarrow B \rightarrow C \rightarrow T \rightarrow T$ 를 거쳐서 AC한다.
길이가 4인 String을 AC하기 위해 5개의 상태를 방문했다.
그러면 위에서 본 비둘기집 원리에 의해 2번 방문한 상태가 적어도 하나 있을 것이다.
실제로 $T$상태를 2번 방문했다.
그렇기 때문에 무한한 길이를 가지는 String ($\in L3$)를 AC할 수 있다.

반면 위 그림은 $\lambda$만 AC가능한 DFA이다.
상태는 2개인데 길이가 0인 $\lambda$(빈 문자열)만 AC하므로 Pumping Lemma를 적용할 수 없다.
Proof of Pumping Lemma
DFA가 상태 $q_1, q_2, \dots, q_N$을 가진다고 하자.
해당 DFA가 길이가 $N$인 String을 AC했다면 적어도 $N+1$개의 상태를 방문했을 것이다.
그 방문 경로를 $r_1, r_2, \dots, r_N, r_{N+1}$이라고 하자.
그럼 비둘기집 원리에 의해 $r_i $~$ r_j$가 반복했을 것이다. ($i<=j$)
예를 들어 $A \rightarrow B \rightarrow C \rightarrow B \rightarrow C \rightarrow D$라면 $B, C$를 반복해서 방문했다.
그 반복한 경로를 $y$, 반복하기 전 경로를 $x$, 반복한 후의 경로를 $z$라고 하면 $|y| > 0$이다.
즉 $x = A$, $y = B \rightarrow C$, $z = D$가 된다.
AC한 경로를 $xyz$라고 하면 $xy^2z, xy^3z, \dots$도 AC할 수 있으므로 무한한 길이의 String을 AC할 수 있다. $\Box$
즉 X3에서 $1010$을 AC했기 때문에 $10100, 101000, 1010000, \dots$도 모두 AC할 수 있다.
Proof using Pumping Lemma
지난시간에 본 Problem X5를 AC하는 DFA가 없다는 것을 Pumping Lemma를 사용해서 증명해보자.
귀류법을 사용해서 Problem X5를 AC하는 DFA가 있다고 하자.
그럼 $ 0^n1^n = xyz$로 분해 가능하다.
한번 더 분해해서 $xyz = xyz'1^n$으로 분해하면 $xyz' = 0^n$이 된다.
Pumping Lemma에 의해 DFA는 $xz', xyz', xy^2z', \dots$를 모두 AC한다.
하지만 $|y| > 0$이므로 $xz', xy^2z', \dots$는 $0^n$이 아니다. (길이가 다름)
이는 문제 조건에 위배되므로 해당 DFA는 존재하지 않는다.
가정에 모순되므로 Problem X5를 AC하는 DFA는 존재하지 않는다. $\Box$
'기타 > 암호학' 카테고리의 다른 글
| [암호학] 10. Push Down Automata (0) | 2022.12.30 |
|---|---|
| [암호학] 9. Non-Deterministic Finite Automata (NFA) (0) | 2022.12.27 |
| [암호학] 7. Deterministic Finite Automata (DFA) (0) | 2022.12.20 |
| [암호학] 6. 프로그래밍 언어론 (4) | 2022.12.16 |
| [암호학] 5. 집합론 2 (0) | 2022.12.13 |